Граф Мередита
| Граф Мередита | |
|---|---|
 | |
| Назван в честь | Гая Мередита |
| Вершин | 70 |
| Рёбер | 140 |
| Диаметр | 8 |
| Обхват | 5 |
| Автоморфизмы | 38698352640 |
| Хроматическое число | 3 |
| Хроматический индекс | 5 |
| Свойства | Эйлеров |
| Книжная толщина | 3 |
| Число очередей | 2 |
Граф Мередита — 4-регулярный неориентированный граф с 70 вершинами и 140 рёбрами, обнаруженный Гаем Мередитом в 1973 году[1].
Граф Мередита вершинно 4-связен и рёберно 4-связен. Имеет хроматическое число 3, хроматический индекс 5, радиус 7, диаметр 8, обхват 4 и он не гамильтонов[2]. Граф имеет книжную толщину 3 и число очередей 2[3].
Опубликованный в 1973 году граф представил контрпример гипотезе Криспина Нэша-Уильямса, что любой 4-регулярный вершинно 4-связный граф всегда гамильтонов[4][5]. Тем не менее, Татт показал, что все 4-связные планарные графы гамильтоновы[6].
Характеристический многочлен графа Мередита равен
- [math]\displaystyle{ (x-4) (x-1)^{10} x^{21} (x+1)^{11} (x+3) (x^2-13) (x^6-26 x^4+3 x^3+169 x^2-39 x-45)^4 }[/math].
Галерея
-
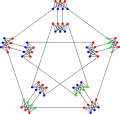
Хроматическое число графа Мередита равно 3.
-
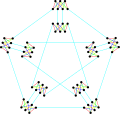
Хроматический индекс графа Мередита равен 5.
Примечания
- ↑ Weisstein, Eric W. Meredith graph (англ.) на сайте Wolfram MathWorld.
- ↑ Bondy J. A., Murty U. S. R. Graph Theory. — Springer, 2007. — С. 470.
- ↑ Jessica Wolz, Engineering Linear Layouts with SAT. Master Thesis, University of Tübingen, 2018
- ↑ Meredith G. H. J. Regular 4-Valent 4-Connected Nonhamiltonian Non-4-Edge-Colorable Graphs // J. Combin. Th.. — 1973. — Вып. B 14. — С. 55—60.
- ↑ Bondy J. A., Murty U. S. R. Graph Theory with Applications. — New York: North Holland, 1976. — С. 239.
- ↑ Recent Progress in Combinatorics / Tutte W.ЛитератураT.. — New York: Academic Press, 1969.
Ссылки
- A.E. Brouwer’s website: The Armanios-Wells graph Архивная копия от 14 апреля 2018 на Wayback Machine
Для улучшения этой статьи желательно: |